Five-limit tuning
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as Template:Nobreak.
Powers of 2 represent intervallic movements by octaves. Powers of 3 represent movements by intervals of perfect fifths (plus one octave, which can be removed by multiplying by 1/2, i.e., 2−1). Powers of 5 represent intervals of major thirds (plus two octaves, removable by multiplying by 1/4, i.e., 2−2). Thus, 5-limit tunings are constructed entirely from stacking of three basic purely-tuned intervals (octaves, thirds and fifths). Since the perception of consonance seems related to low numbers in the harmonic series, and 5-limit tuning relies on the three lowest primes, 5-limit tuning should be capable of producing very consonant harmonies. Hence, 5-limit tuning is considered a method for obtaining just intonation.
The number of potential intervals, pitch classes, pitches, key centers, chords, and modulations available to 5-limit tunings is unlimited, because no (nonzero integral) power of any prime equals any power of any other prime, so the available intervals can be imagined to extend indefinitely in a 3-dimensional lattice (one dimension, or one direction, for each prime). If octaves are ignored, it can be seen as a 2-dimensional lattice of pitch classes (note names) extending indefinitely in two directions.
However, most tuning systems designed for acoustic instruments restrict the total number of pitches for practical reasons. It is also typical (but not always done) to have the same number of pitches in each octave, representing octave transpositions of a fixed set of pitch classes. In that case, the tuning system can also be thought of as an octave-repeating scale of a certain number of pitches per octave.
The frequency of any pitch in a particular 5-limit tuning system can be obtained by multiplying the frequency of a fixed reference pitch chosen for the tuning system (such as A440, A442, A432, C256, etc.) by some combination of the powers of 3 and 5 to determine the pitch class and some power of 2 to determine the octave.
For example, if we have a 5-limit tuning system where the base note is C256 (meaning it has 256 cycles per second and we decide to call it C), then fC = 256 Hz, or "frequency of C equals 256 Hz." There are several ways to define E above this C. Using thirds, one may go up one factor 5 and down two factors 2, reaching a frequency ratio of 5/4, or using fifths one may go up four factors of 3 and down six factors of 2, reaching 81/64. The frequencies become:
or
Diatonic scale[edit | edit source]
Assuming we restrict ourselves to seven pitch classes (seven notes per octave), it is possible to tune the familiar diatonic scale using 5-limit tuning in a number of ways, all of which make most of the triads ideally tuned and as consonant and stable as possible, but leave some triads in less-stable intervalic configurations.
The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major, the ratio of the frequencies of the notes G to D (a perfect fifth) is 3/2, while that of G to C is 2/3 (a descending perfect fifth) or 4/3 (a perfect fourth) going up, and the major third G to B is 5/4.

A just diatonic scale may be derived as follows. Imagining the key of C major, suppose we insist that the subdominant root F and dominant root G be a fifth (3:2) away from the tonic root C on either side, and that the chords FAC, CEG, and GBD be just major triads (with frequency ratios 4:5:6):
| Tone | Name | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 | |||||||||
| Natural | 24 | 27 | 30 | 32 | 36 | 40 | 45 | 48 | |||||||||
| Cents | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 | |||||||||
| Step | Interval | T | t | s | T | t | T | s | |||||||||
| Ratio | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||||
| Cents step | 204 | 182 | 112 | 204 | 182 | 204 | 112 | ||||||||||
This is known as Ptolemy's intense diatonic scale. Here the row headed "Natural" expresses all these ratios using a common list of natural numbers (by multiplying the row above by the lcm of its denominators). In other words, the lowest occurrence of this one-octave scale shape within the harmonic series is as a subset of 7 of the 24 harmonics found in the octave from harmonics 24 to 48.
The three major thirds are correct (5:4), and three of the minor thirds are as expected (6:5), but D to F is a semiditone or Pythagorean minor third (equal to three descending just perfect fifths, octave adjusted), a syntonic comma narrower than a justly tuned (6:5) minor third.
As a consequence, we obtain a scale in which EGB and ACE are just minor triads (10:12:15), but the DFA triad doesn't have the minor shape or sound we might expect, being (27:32:40). Furthermore, the BDF triad is not the (25:30:36) diminished triad that we would get by stacking two 6:5 minor thirds, being (45:54:64) instead:[1][2]
It can be seen that basic step-wise scale intervals appear:
- s = 16:15 (Semitone)
- t = 10:9 (Minor tone)
- T = 9:8 (Major tone)
Which may be combined to form larger intervals (among others):
- Ts = 6:5 (minor third)
- Tt = 5:4 (major third)
- Tts = 4:3 (perfect fourth)
- TTts = 3:2 (perfect fifth)
- TTTttss 2:1 (octave)
Another way to do it is as follows. Thinking in the relative minor key of A minor and using D, A, and E as our spine of fifths, we can insist that the chords DFA, ACE, and EGB be just minor triads (10:12:15):
| Tone | Name | A | B | C | D | E | F | G | A | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 6/5 | 4/3 | 3/2 | 8/5 | 9/5 | 2/1 | |||||||||
| Natural | 120 | 135 | 144 | 160 | 180 | 192 | 216 | 240 | |||||||||
| Cents | 0 | 204 | 316 | 498 | 702 | 814 | 1018 | 1200 | |||||||||
| Step | Interval | T | s | t | T | s | T | t | |||||||||
| Ratio | 9/8 | 16/15 | 10/9 | 9/8 | 16/15 | 9/8 | 10/9 | ||||||||||
| Cents step | 204 | 112 | 182 | 204 | 112 | 204 | 182 | ||||||||||
If we contrast that against the earlier scale, we see that for five pairs of successive notes the ratios of the steps remain the same, but one note, D, the steps C-D and D-E have switched their ratios.
The three major thirds are still 5:4, and three of the minor thirds are still 6:5 with the fourth being 32:27, except that now it's BD instead of DF that is 32:27. FAC and CEG still form just major triads (4:5:6), but GBD is now (108:135:160), and BDF is now (135:160:192).
There are other possibilities such as raising A instead of lowering D, but each adjustment breaks something else.
It is evidently not possible to get all seven diatonic triads in the configuration (4:5:6) for major, (10:12:15) for minor, and (25:30:36) for diminished at the same time if we limit ourselves to seven pitches.
That demonstrates the need for increasing the numbers of pitches to execute the desired harmonies in tune.
Twelve tone scale[edit | edit source]
To build a twelve tone scale in 5-limit tuning, we start by constructing a table containing fifteen justly intonated pitches:
| Factor | 1/9 | 1/3 | 1 | 3 | 9 | |
|---|---|---|---|---|---|---|
| 5 | note ratio cents |
D− 10/9 182[3] |
A 5/3 884 |
E 5/4 386 |
B 15/8 1088 |
F♯+ 45/32 590[3] |
| 1 | note ratio cents |
B♭− 16/9 996[3] |
F 4/3 498 |
C 1 0 |
G 3/2 702 |
D 9/8 204 |
| 1/5 | note ratio cents |
G♭− 64/45 610[3] |
D♭− 16/15 112[3] |
A♭ 8/5 814 |
E♭ 6/5 316 |
B♭ 9/5 1018 |
The factors listed in the first row and column are powers of 3 and 5, respectively (e.g., 1/9 = 3−2). Colors indicate couples of enharmonic notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps:
- For each cell of the table, a base ratio is obtained by multiplying the corresponding factors. For instance, the base ratio for the lower-left cell is 1/9 · 1/5 = 1/45.
- The base ratio is then multiplied by a negative or positive power of 2, as large as needed to bring it within the range of the octave starting from C (from 1/1 to 2/1). For instance, the base ratio for the lower left cell (1/45) is multiplied by 25, and the resulting ratio is 64/45, which is a number between 1/1 and 2/1.
Note that the powers of 2 used in the second step may be interpreted as ascending or descending octaves. For instance, multiplying the frequency of a note by 25 means increasing it by 5 octaves. Moreover, each row of the table may be considered a sequence of fifths (ascending to the right), and each column a sequence of major thirds (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, you can obtain A (5/3 ratio), starting from C, by moving one cell to the left and one upward in the table, which means descending by one fifth (2/3) and ascending by one major third (5/4):
Since this is below C, you need to move up by an octave to end up within the desired range of ratios (from 1/1 to 2/1):
A 12 tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of G♭, according to a convention valid even for C-based Pythagorean and 1/4-comma meantone scales. Note that it is a diminished fifth, close to half an octave, above the tonic C, which is a disharmonic interval; also its ratio has the largest values in its numerator and denominator of all tones in the scale, which make it least harmonious: all reasons to avoid it.
The first strategy, which we operationally denote here as symmetric scale 1, consists of selecting for removal the tones in the upper left and lower right corners of the table. The second one, denoted as symmetric scale 2, consists of discarding the notes in the first and last cell of the second row (labeled "1"). The third one, denoted as asymmetric scale, consists of discarding the first column (labeled "1/9"). The resulting 12-tone scales are shown below:
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In the first and second scale, B♭ and D are exactly the inversion of each other. This is not true for the third one. This is the reason why these two scales are regarded as symmetric (although the removal of G♭ makes all 12 tone scales, including those produced with any other tuning system, slightly asymmetric).
The asymmetric system has the advantage of having the "justest" ratios (those containing smaller numbers), nine pure fifths (factor 3/2), eight pure major thirds (factor 5/4) by design, but also six pure minor thirds (factor 6/5). However, it also contains two impure fifths (e.g., D to A is 40/27 rather than 3/2) and three impure minor thirds (e.g., D to F is 32/27 rather than 6/5), which practically limits modulation to a narrow range of keys. The chords of the tonic C, dominant G and subdominant F are pure, as well as D♭, A♭, E♭ and the minor chords Fm, Cm, Gm, Am, Bm and Em, but not the Dm.
A drawback of the asymmetric system is that it produces 14 wolf intervals, rather than 12 as for the symmetric ones (see below).
The B♭ in the first symmetric scale differs from the B♭ in the other scales by the syntonic comma, being over 21 cents. In equally tempered scales, the difference is eliminated by making all steps the same frequency ratio.
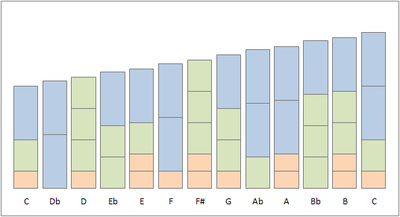 |
The construction of the asymmetric scale is graphically shown in the picture. Each block has the height in cents of the constructive frequency ratios 2/1, 3/2 and 5/4. Recurring patterns can be recognised. For example, many times the next note is created by replacing a 5/4-block and a 3/2-block by a 2/1-block, representing a ratio of 16/15.
For a similar image, built using frequency factors 2, 3, and 5, rather than 2/1, 3/2, and 5/4, see here.
The justest ratios[edit | edit source]
The just ratios used to build these scales can be used as a reference to evaluate the consonance of intervals in other scales (for instance, see this comparison table). However, 5-limit tuning is not the only method to obtain just intonation. It is possible to construct just intervals with even "juster" ratios, or alternately, with values closer to the equal-tempered equivalents. For instance, a 7-limit tuning is sometimes used to obtain a slightly juster and consequently more consonant interval for the minor seventh (7/4) and its inversion, the major second (8/7). A list of these reference ratios, which may be referred to as pure or strictly just intervals or ratios, is provided below:
| Interval name | Short | Number of semitones |
5-limit tuning | 7-limit tuning | 17-limit tuning | |||
|---|---|---|---|---|---|---|---|---|
| Symmetric scales | Asymmetric scales | |||||||
| N. 1 | N. 2 | Standard | Extended | |||||
| Perfect unison | P1 | 0 | 1/1 | 1/1 | 1/1 | 1/1 | 1/1 | 1/1 |
| Minor second | m2 | 1 | 16/15 | 16/15 | 16/15 | 16/15 | 15/14 | 14/13 |
| Major second | M2 | 2 | 9/8 | 10/9 | 9/8 | 9/8 | 8/7 | 8/7 |
| Minor third | m3 | 3 | 6/5 | 6/5 | 6/5 | 6/5 | 6/5 | 6/5 |
| Major third | M3 | 4 | 5/4 | 5/4 | 5/4 | 5/4 | 5/4 | 5/4 |
| Perfect fourth | P4 | 5 | 4/3 | 4/3 | 4/3 | 4/3 | 4/3 | 4/3 |
| Augmented fourth | A4 | 6 | 45/32 | 45/32 | 45/32 | 25/18 | 7/5 | 7/5 or 17/12 |
| Diminished fifth | d5 | 6 | 64/45 | 64/45 | 64/45 | 36/25 | 10/7 | 10/7 or 24/17 |
| Perfect fifth | P5 | 7 | 3/2 | 3/2 | 3/2 | 3/2 | 3/2 | 3/2 |
| Minor sixth | m6 | 8 | 8/5 | 8/5 | 8/5 | 8/5 | 8/5 | 8/5 |
| Major sixth | M6 | 9 | 5/3 | 5/3 | 5/3 | 5/3 | 5/3 | 5/3 |
| Minor seventh | m7 | 10 | 16/9 | 9/5 | 9/5 | 9/5 | 7/4 | 7/4 |
| Major seventh | M7 | 11 | 15/8 | 15/8 | 15/8 | 15/8 | 15/8 | 13/7 |
| Perfect octave | P8 | 12 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 |
Cells highlighted in yellow indicate intervals that are juster than those in the non-coloured cells in the same row. Those highlighted in cyan indicate even juster ratios.
Notice that the ratios 45/32 and 64/45 for the tritones (augmented fourth and diminished fifth) are not in all contexts regarded as strictly just, but they are the justest possible in the above-mentioned 5-limit tuning scales. An extended asymmetric 5-limit scale (see below) provides slightly juster ratios for both the tritones (25/18 and 36/25), the purity of which is also controversial. 7-limit tuning allows for the justest possible ratios, namely 7/5 (about 582.512 cents, also known as septimal tritone) and 10/7 (about 617.488 cents). These ratios are more consonant than 17/12 (about 603.000 cents) and 24/17 (about 597.000 cents), which can be obtained in 17-limit tuning, yet the latter are also fairly common, as they are closer to the equal-tempered value of 600.000 cents.
The above-mentioned 7/4 interval (about 968.826 cents), also known as the septimal minor seventh, or harmonic seventh, has been a contentious issue throughout the history of music theory; it is 31 cents flatter than an equal-tempered minor seventh.
Size of intervals[edit | edit source]
The tables above show only the frequency ratios of each tone with respect to the base note C. However, intervals can be formed by starting from each of the twelve notes. Thus, twelve intervals can be defined for each interval type (twelve unisons, twelve semitones, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).
In 5-limit tuning, each of the interval types, except for the unisons and the octaves, has three or even four different sizes. This is the price paid for seeking just intonation. The tables on the right and below show their frequency ratios and their approximate sizes in cents, for the "asymmetric scale". Similar tables, for the "symmetric scale 1", are published here and here. Interval names are given in their standard shortened form. For instance, the size of the interval from C to G, which is a perfect fifth (P5), can be found in the seventh column of the row labeled C. Pure intervals, as defined above, are shown in bold font (notice that, as explained above, the justly intonated ratio 45/32 ≈ 590 cents, for A4, is not considered pure).
A color code distinguishes intervals that deviate from the reference sizes in the construction table, and show the amount of their deviation. Wolf intervals are marked in black.[4]
The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, the frequencies defined by construction for the twelve notes determine four different semitones (i.e., intervals between adjacent notes). For instance:
-
("Just" augmented unison between E♭ and E) -
(Augmented unison between D♭ and D) -
("Just" minor second between C and D♭) -
(Minor second between A and B♭)
Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly
As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.
Note that 5-limit tuning was designed to maximize the number of pure intervals, but even in this system several intervals are markedly impure (for instance, as shown in the figures, 60 out of 144 intervals deviate by at least 19.6 cents from the justly intonated reference sizes shown in the construction table). Also, 5-limit tuning yields a much larger number of wolf intervals with respect to Pythagorean tuning, which can be considered a 3-limit just intonation tuning. Namely, while Pythagorean tuning determines only 2 wolf intervals (a fifth and a fourth), the 5-limit symmetric scales produce 12 of them, and the asymmetric scale 14. It is also important to note that the two fifths, three minor thirds, and three major sixths marked in orange in the tables (ratio 40/27, 32/27, and 27/16 (or G−, E♭−, and A+[3]), even though they do not completely meet the conditions[4] to be wolf intervals, deviate from the corresponding pure ratio by an amount (1 syntonic comma, i.e., 81/80, or about 21.5 cents) large enough to be clearly perceived as dissonant.[5]
Clearly, the more we try to increase the number of pure and consonant intervals, the more the remaining ones become impure and dissonant, by compensation. Some of the major seconds (M2) and minor sevenths (m7) represent the only exception to this rule. As you can see in the tables, those marked in orange are pure (10/9 and 16/9), even if their size is 81/80 narrower than the corresponding reference size (9/8 and 9/5).
For a comparison with other tuning systems, see also this table.
Commas[edit | edit source]
In other tuning systems, a comma may be defined as a minute interval, equal to the difference between two kinds of semitones (diatonic and chromatic, also known as minor second, m2, or augmented unison, A1). In this case, however, 4 different kinds of semitones are produced (two A1, S1 and S2, and two m2, S3 and S4), and 12 different commas can be defined as the differences between their sizes in cents, or equivalently as the ratios between their ratios. Among these, we select the six ascending ones (those with ratio larger than 1/1, and positive size in cents):
| Name of comma | Equivalent definitions | Size | ||
|---|---|---|---|---|
| In meantone temperament | In 5-limit tuning (asymmetric scale) |
Ratio | Cents | |
| Diaschisma (DS) | in 1/6-comma meantone |
|||
| Syntonic comma (SC) | ||||
| Lesser diesis (LD) | in 1/4-comma meantone |
|||
| Greater diesis (GD) | in 1/3-comma meantone |
|||
The other six ratios are discarded because they are just the opposite of these, and hence they have exactly the same length, but an opposite direction (i.e., a descending direction, a ratio smaller than 1/1, and a negative size in cents). We obtain commas of four different sizes: the diaschisma, the lesser diesis, the syntonic comma, and the greater diesis. Since S1 (the just A1) and S3 (the just m2) are the most often occurring semitones in this 12-tone scale (see tables above), the lesser diesis, being defined as the ratio between them, is the most often observed comma.
The syntonic comma is also defined, in 5-limit tuning, as the ratio between the major tone (M2 with size 9/8) and the minor tone (M2 with size 10/9). Notice that it cannot be defined, in other tuning systems, as the ratio between diatonic and cromatic semitones (m2/A1), but it is an important reference value used to tune the perfect fifth in any tuning system in the syntonic temperament continuum (including also meantone temperaments).
Diminished seconds[edit | edit source]
Three of the above-mentioned commas, namely the diaschisma, the diesis and the greater diesis, meet the definition of the diminished second, being the difference between the sizes in cents of a diatonic and a chromatic semitone (or equivalently the ratio between their frequency ratios).
On the contrary, the syntonic comma is defined either as the difference in cents between two chromatic semitones (S2 and S1), or between two diatonic semitones (S4 and S3), and cannot be considered a diminished second.
Extension of the twelve-tone scale[edit | edit source]
The table above uses only low powers of 3 and 5 to build the base ratios. However, it can be easily extended by using higher positive and negative powers of the same numbers, such as 52 = 25, 5−2 = 1/25, 33 = 27, or 3−3 = 1/27. A scale with 25, 35, or even more pitches can be obtained by combining these base ratios.
For instance, one can obtain 35 pitches by adding rows in each direction like this:
| Factor | 1/9 | 1/3 | 1 | 3 | 9 | |
|---|---|---|---|---|---|---|
| 125 | note ratio cents |
A♯ 125/72 955.0[3] |
E♯ 125/96 457.0 |
B♯ 125/64 1158.9 |
F 375/256 660.9[3] |
C 1125/1024 162.9[3] |
| 25 | note ratio cents |
F♯ 25/18 568.7[3] |
C♯ 25/24 70.7 |
G♯ 25/16 772.6 |
D♯ 75/64 274.6 |
A♯+ 225/128 976.5[3] |
| 5 | note ratio cents |
D− 10/9 182.4 |
A 5/3 884.4 |
E 5/4 386.3 |
B 15/8 1088.3 |
F♯+ 45/32 590.2 |
| 1 | note ratio cents |
B♭− 16/9 996.1 |
F 4/3 498.0 |
C 1/1 0.0 |
G 3/2 702.0 |
D 9/8 203.9 |
| 1/5 | note ratio cents |
G♭− 64/45 609.8 |
D♭− 16/15 111.7 |
A♭ 8/5 813.7 |
E♭ 6/5 315.6 |
B♭ 9/5 1017.6 |
| 1/25 | note ratio cents |
E 256/225 223.5[3] |
B 128/75 925.4[3] |
F♭ 32/25 427.4 |
C♭ 48/25 1129.3 |
G♭ 36/25 631.3 |
| 1/125 | note ratio cents |
C 2048/1125 1037.1[3] |
G 512/375 539.1[3] |
D 128/125 41.1[3] |
A 192/125 743.0 |
E 144/125 245.0 |
The left column (1/9) is sometimes removed (as in the asymmetric scale shown above), thus creating an asymmetric table with a smaller number of pitches. Notice that a juster ratio is produced for the diminished fifth (C-G♭ = 36/25), with respect to the restricted 5-limit tuning described above (where C to G♭- = 64/45).[6]
History[edit | edit source]
In Pythagorean tuning, perhaps the first tuning system theorized in the West,[7] the only highly consonant intervals were the perfect fifth and its inversion, the perfect fourth. The Pythagorean major third (81:64) and minor third (32:27) were dissonant, and this prevented musicians from using triads and chords, forcing them for centuries to write music with relatively simple texture. In late Middle Ages, musicians realized that by slightly tempering the pitch of some notes, the Pythagorean thirds could be made consonant. For instance, if you decrease by a syntonic comma (81:80) the frequency of E, C-E (a major third), and E-G (a minor third) become just. Namely, C-E is narrowed to a justly intonated ratio of
and at the same time E-G is widened to the just ratio of
The drawback is that the fifths A-E and E-B, by flattening E, become almost as dissonant as the Pythagorean wolf fifth. But the fifth C-G stays consonant, since only E has been flattened (C-E * E-G = 5/4 * 6/5 = 3/2), and can be used together with C-E to produce a C-major triad (C-E-G).
By generalizing this simple rationale, Gioseffo Zarlino, in the late sixteenth century, created the first justly intonated 7-tone (diatonic) scale, which contained pure perfect fifths (3:2), pure major thirds, and pure minor thirds:
F → A → C → E → G → B → D
This is a sequence of just major thirds (M3, ratio 5:4) and just minor thirds (m3, ratio 6:5), starting from F:
F + M3 + m3 + M3 + m3 + M3 + m3
Since M3 + m3 = P5 (perfect fifth), i.e., 5/4 * 6/5 = 3/2, this is exactly equivalent to the diatonic scale obtained in 5-limit just intonation, and hence can be viewed as a subset of the construction table used for the 12-tone (chromatic) scale:
| A | → | E | → | B | ||
| ↑ | ↑ | ↑ | ||||
| F | → | C | → | G | → | D |
where both rows are sequences of just fifths, and F-A, C-E, G-B are just major thirds:
| M3 | M3 | M3 | ||||
| + | + | + | ||||
| F | + | P5 | + | P5 | + | P5 |
See also[edit | edit source]
- Mathematics of musical scales
- Microtonal music
- Microtuner
- Pythagorean interval
- Semitone
- List of intervals in 5-limit just intonation
- List of meantone intervals
- List of musical intervals
- List of pitch intervals
- Whole-tone scale
- Regular number
- Hexany
- Electronic tuner
- Consonance and dissonance
Notes[edit | edit source]
- ↑ Wright, David (2009). Mathematics and Music, pp. 140–41. ISBN 978-0-8218-4873-9.
- ↑ Johnston, Ben and Gilmore, Bob (2006). "A Notation System for Extended Just Intonation" (2003), "Maximum clarity" and Other Writings on Music, p.78. ISBN 978-0-252-03098-7.
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 3.11 3.12 3.13 3.14 3.15 John Fonville. "Ben Johnston's Extended Just Intonation- A Guide for Interpreters", pp. 113–14, Perspectives of New Music, Vol. 29, No. 2 (Summer, 1991), pp. 106–137.
- ↑ 4.0 4.1 Wolf intervals are operationally defined herein as intervals composed of 3, 4, 5, 7, 8, or 9 semitones (i.e., major and minor thirds or sixths, perfect fourths or fifths, and their enharmonic equivalents) the size of which deviates by more than one syntonic comma (about 21.5 cents) from the corresponding justly intonated interval. Intervals made up of 1, 2, 6, 10, or 11 semitones (e.g., major and minor seconds or sevenths, tritones, and their enharmonic equivalents) are considered dissonant even when they are justly tuned, thus they are not marked as wolf intervals even when they deviate from just intonation by more than one syntonic comma.
- ↑ See this article, retrieved on July 30, 2010 from the newmusicbox.org web site.
- ↑ The notes from G♯ down to D♭ are taken from Don Michael Randel, The Harvard Dictionary of Music, Fourth Edition. Cambridge, MA: Belknap Press, 2003, p. 415.
Furthermore, regarding the notes from Fdown to D♭, the Tonalsoft Encyclopedia of Microtonal Music Theory states: "In fact this structure perfectly describes Salinas's just-intonation structure."
- ↑ The oldest known description of the Pythagorean tuning system appears in Babylonian artifacts. See: West, M.L.. The Babylonian Musical Notation and the Hurrian Melodic Texts, Music & Letters vol. 75 no. 2 (May 1994). pp. 161-179.
External links[edit | edit source]
- Art of the States: microtonal/just intonation works using just intonation by American composers
- The Chrysalis Foundation – Just Intonation: Two Definitions
- Dante Rosati's 21 Tone Just Intonation guitar
- Just Intonation by Mark Nowitzky
- Just Intonation Explained by Kyle Gann
- A selection of Just Intonation works edited by the Just Intonation Network web published on the Tellus Audio Cassette Magazine project archive at Ubuweb
- Medieval Music and Arts Foundation
- Music Novatory – Just Intonation
- Why does Just Intonation sound so good?
- The Wilson Archives
- Barbieri, Patrizio. Enharmonic instruments and music, 1470–1900. (2008) Latina, Il Levante
- 22 Note Just Intonation Keyboard Software with 12 Indian Instrument Sounds Libreria Editrice
- Plainsound Music Edition – JI music and research, information about the Helmholtz-Ellis JI Pitch Notation
| This article uses material from Five-limit tuning on Wikipedia (view authors). License under CC BY-SA 3.0. |








![{\displaystyle S_E = \sqrt[12]{2} = 100.000 \ \hbox{cents}. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c3bd6bd5633521627e9dd9016b063f4ca092196)




















